要想提高中考成绩，那么如何做好中考数学的复习，特别是针对压轴题的复习，成为了大家都绕不开的话题。

压轴题一般是指在试卷当中最后面出现的综合题，此类题型一般具有分值较高、难度大、综合能力强等特点，因其在考试中能够拉开考生的学习成绩，自然成为很多中考命题老师青睐的对象。

我们认真研究一些压轴题，会发现全国很多的中考数学试卷都喜欢考动点类的压轴题，这些与动点相关的压轴题都具有知识点多、题型复杂、解法灵活等鲜明特点，在一定程度上提升了中考数学的难度，成为选拔考生的一个常考热点。

在众多动点问题当中，与几何相关的动点题型历来都是中考数学试题的热点题型。如以直角三角形为载体的动点问题，其立意新颖，集几何、代数知识于一体，数形结合，有较强的综合性。既能考查学生的创造性思维品质，又能体现学生的实际水平和应变能力。

直角三角形相关的动点压轴题，讲解分析1：

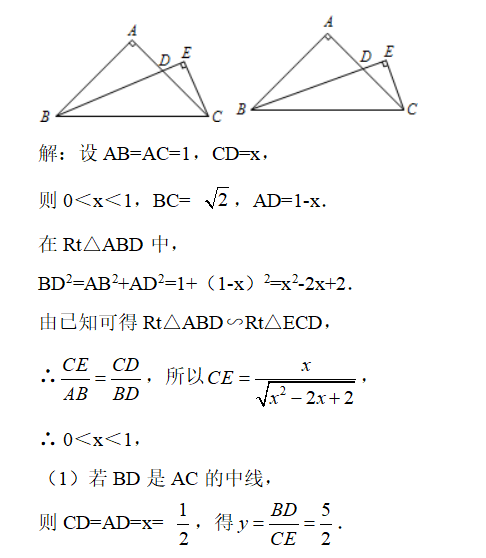
已知△ABC是等腰直角三角形，∠A=90°，D是腰AC上的一个动点，过C作CE垂直于BD或BD的延长线，垂足为E，如图．

（1）若BD是AC的中线，求BD/CE的值；

（2）若BD是∠ABC的角平分线，求BD/CE的值；

（3）结合（1）、（2），试推断BD/CE的取值范围（直接写出结论，不必证明），并探究BD/CE的值能小于4/3吗？若能，求出满足条件的D点的位置；若不能，说明理由．

考点分析：

相似三角形的判定与性质；勾股定理；等腰直角三角形；解直角三角形；几何综合题．

题干分析：

先设AB=AC=1，CD=x，则0＜x＜1，求得BC的值，AD=1-x．在直角三角形ABD中求得BD得平方，又求得Rt△ABD∽Rt△ECD，

（1）BD是AC的中线，则CD=AD=x=1/2，则解得；

（2）BD是∠ABC的角平分线，则求得x，y值；

（3）由以上两个问题，从BD/CE的比值求得x的值，则求得AD/CD的值．

解题反思：

本题考查了相似三角形的判定和性质，本题从中线，角平分线以及中线与角平线相结合的问题来考查，是一道考查全面的好问题．

动点问题虽然是中考数学常考的题型，但对于大多数学生来说，这可是失分重灾区。要想拿到此类题型的分数，分析运动过程、揭开"动点"问题的神秘面纱，理解并掌握其中的解题方法与解题技巧就显得尤为重要。

直角三角形相关的动点压轴题，讲解分析2：

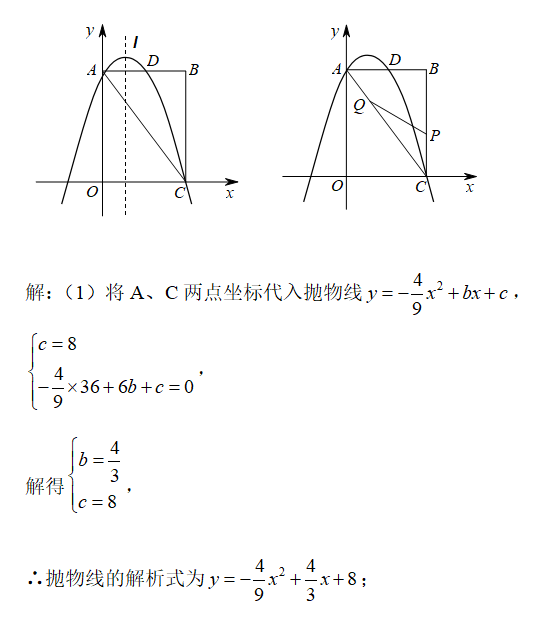
如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线y=-4x2/9+bx+c经过A、C两点，与AB边交于点D．

（1）求抛物线的函数表达式；

（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．

①求S关于m的函数表达式，并求出m为何值时，S取得最大值；

②当S最大时，在抛物线y=-4x2/9+bx+c的对称轴l上若存在点F，使△FDQ为直角三角形，请直接写出所有符合条件的F的坐标；若不存在，请说明理由．

考点分析：

二次函数综合题；代数几何综合题；数形结合。

题干分析：

（1）将A、C两点坐标代入抛物线y=-4x2/9+bx+c，即可求得抛物线的解析式；

（2）①先用m 表示出QE的长度，进而求出三角形的面积S关于m的函数，化简为顶点式，便可求出S的最大值；

②直接写出满足条件的F点的坐标即可，注意不要漏写．

解题反思：

本题是二次函数的综合题，其中涉及的到的知识点有抛物线的公式的求法抛物线的最值等知识点，是各地中考的热点和难点，解题时注意数形结合数学思想的运用，同学们要加强训练，属于中档题．

直角三角形是中考必考的重要内容之一，在填空、选择、解答题中都有可能出现，在解答题中它往往与三角函数、相似三角形等相结合。以直角三角形为载体，除了会考查基础知识，同时又会考查动点、分类讨论思想。

​直角三角形相关的动点压轴题，讲解分析3：

如图，Rt△ABC中，∠A=30°，BC=10cm，点Q在线段BC上从B向C运动，点P在线段BA上从B向A运动．Q、P两点同时出发，运动的速度相同，当点Q到达点C时，两点都停止运动．作PM⊥PQ交CA于点M，过点P分别作BC、CA的垂线，垂足分别为E、F．

（1）求证：△PQE∽△PMF；

（2）当点P、Q运动时，请猜想线段PM与MA的大小有怎样的关系？并证明你的猜想；

（3）设BP=x，△PEM的面积为y，求y关于x的函数关系式，当x为何值时，y有最大值，并将这个值求出来．

考点分析：

相似三角形的判定与性质；二次函数的最值；等边三角形的判定与性质；含30度角的直角三角形；解直角三角形。

题干分析：

（1）由∠EPF=∠QPM=90°，利用互余关系证明△PQE∽△PMF；

（2）相等．运动速度相等，时间相同，则BP=BQ，∠B=60°，△BPQ为等边三角形，可推出∠MPA=∠A=30°，等角对等边；

（3）由面积公式得S△PEM=PE×PF/2，解直角三角形分别表示PE，PF，列出函数式，利用函数的性质求解．

解题反思：

本题考查了相似三角形的判定与性质，等边三角形的判定与性质，解直角三角形，二次函数的性质．关键是根据题意判断相似三角形，利用相似比及解直角三角形得出等量关系。